The first explanation of the lateral deflection of a spinning object was credited by Lord Rayleigh to work done by the German physicist Dr. Heinrich Gustav Magnus in 1852 which we discussed in part one of the Magnus effect.
More Than Just a Ball ⚽
So...you thought a ball is just a "ball"? Nope! There is even more science to the football than you can imagine!
Since 1970, every World Cup football has been made by Adidas - let's have a look at the changes in ball design and their technology. Traditionally, a football is constructed from 32 panels stitched together by hand. But the Teamgeist model had 14 panels glued together with heat (thermally bonded).
It did not take long until the first players complained about the "weird" behaviour during flight. Fast forward, Adidas redesigned the football that should change everything – the Jabulani. Surprisingly, the criticism was even more than with the Teamgeist four years earlier, comparing the Jabulani to a beach ball which flies in a very unpredictable way.
Let us have a closer look at the Adidas Jabulani used for the FIFA World Cup in South Africa 2010. Starting from the infamous 32 panel black and white Telstar introduced in Mexico City in 1970, it was always the goal (no pun intended) to create better balls. At the end of the day, it's the players on the field that need to feel comfortable and the ball should somewhat be predictably in terms of its flight trajectory. But "perfect" may not be good enough...

Spain's Iker Casillas has dissed it as "rotten," while Italy's top goalkeeper Gianluigi Buffon tagged it as "unpredictable."
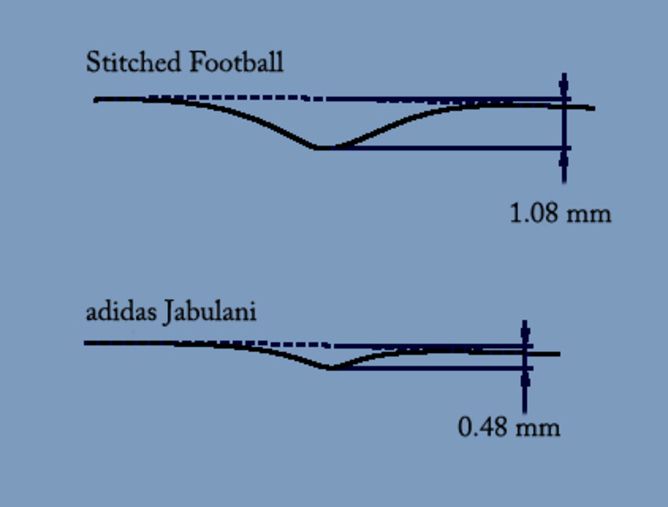
The old school Telstar ball had 32 panels with 20 regular hexagonal and 12 regular pentagonal panels. The Jabulani however had eight heat welded 3D panels.
The decreased of shallow number of seams increased the laminar flow region around the ball with a high drag coefficient, while the drag was decreased at higher speeds. The relatively large width of the laminar regime compared to that of a traditional ball gave it the behaviour of a beach ball for a wider velocity range, which was the subject of complaints from many goalies. Also, the pattern that the ball presents to the wind has an impact on the sudden changes in direction for these “knuckleball” shots.
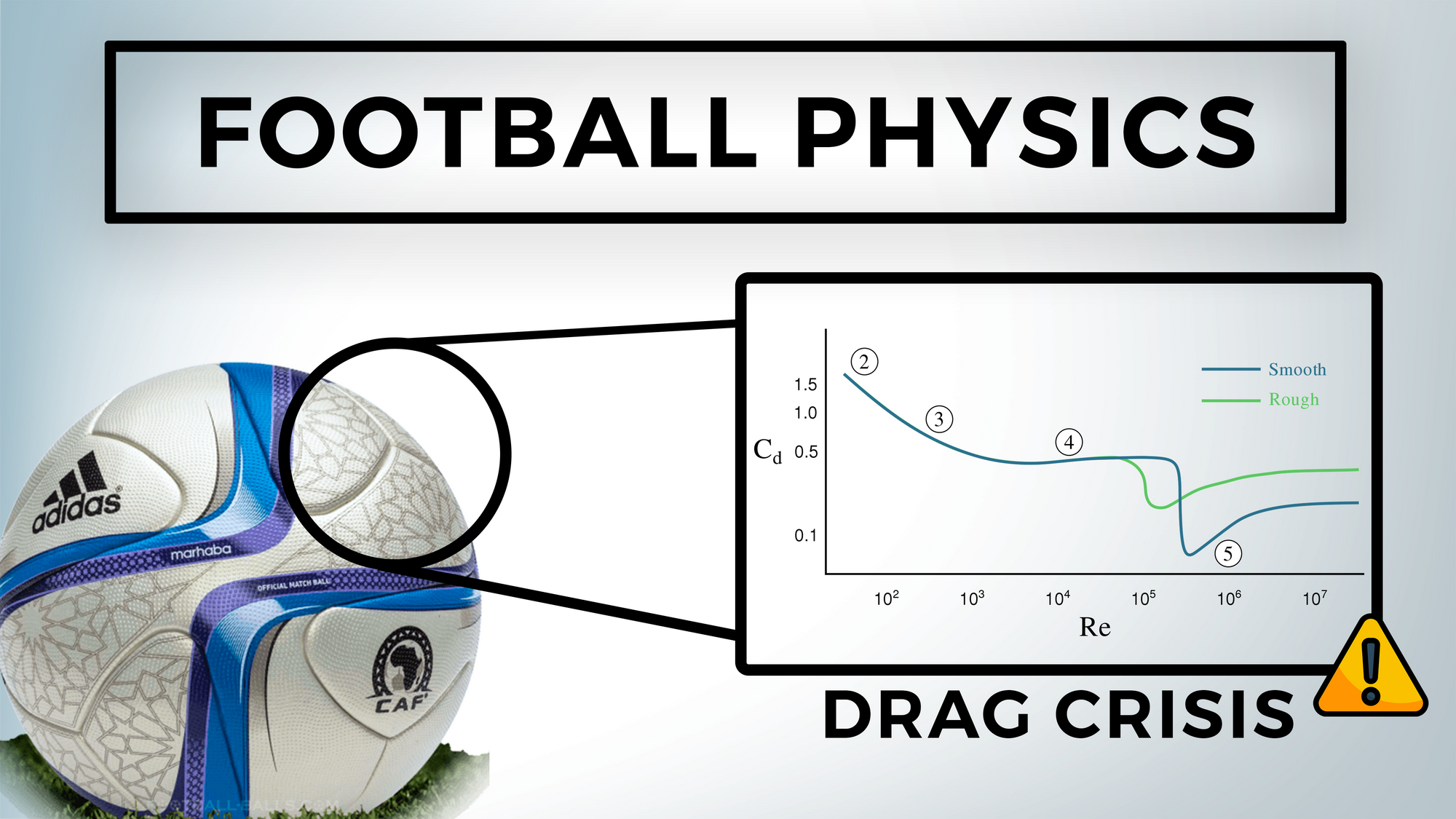
The high drag coefficients for laminar flow are caused by boundary layer separation forming a low-pressure wake that slows down the ball in this flow regime. For higher flight velocities, the boundary layer becomes turbulent ahead of the separation point and remains attached further downstream on the rear side of the ball before the flow reverses. This leads to a narrower wake and a correspondingly lower drag coefficient. The phenomenon is generally referred to as the drag crisis.
The Drag Crisis - A Quick Primer ⚡
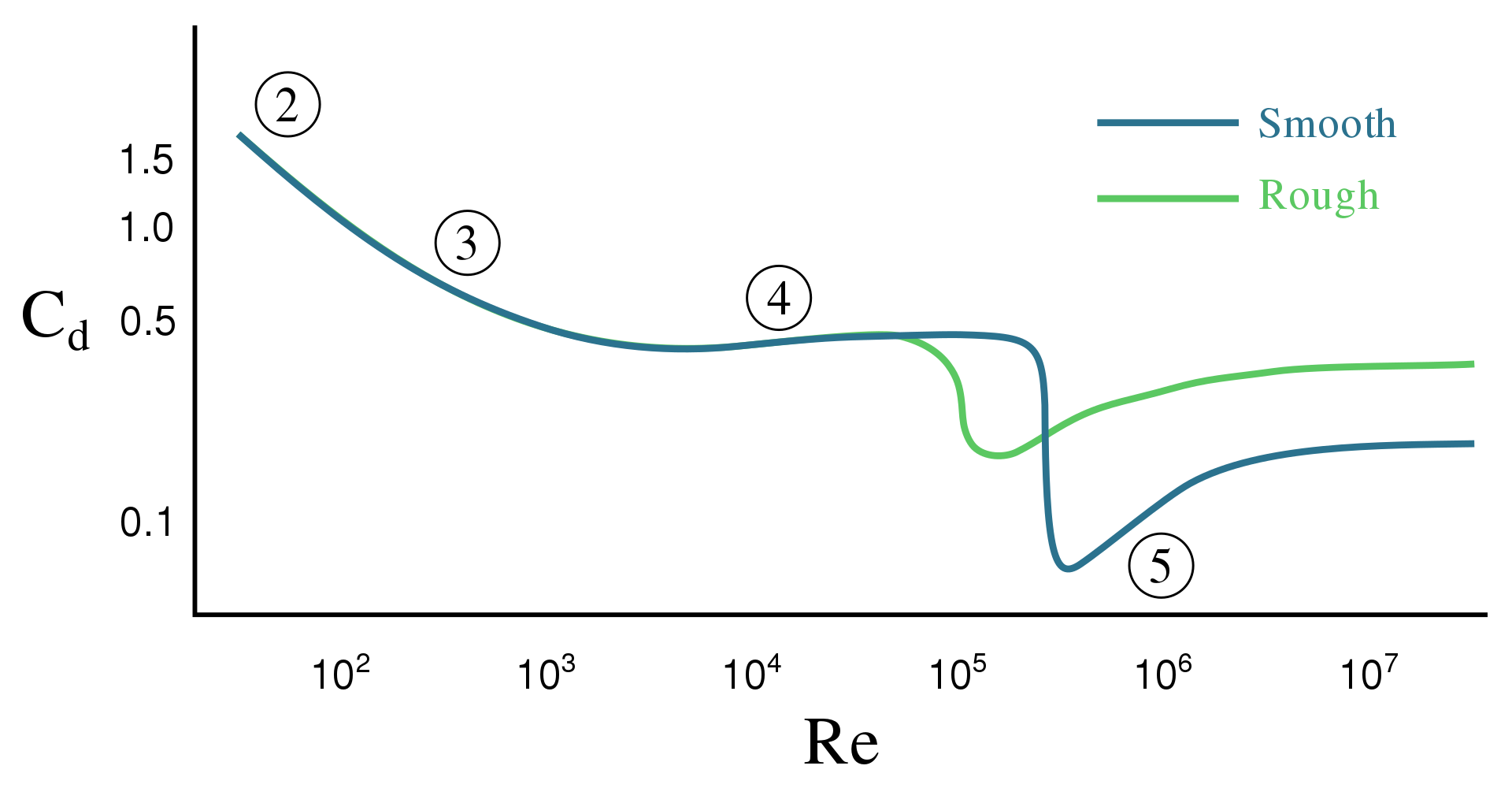
The transition from laminar to turbulent flow occurs at a critical Reynolds number (Re_crit) which depends on details of the system, such as surface roughness.
Normally the drag force increases with speed. In 1912, Gustave Eiffel discovered what is today known as the drag crisis. Studying flow around a smooth sphere, he found a drop in the drag force as the flow speed increased above Reynolds number 200 000 and continued to drop until about Re = 300,000 (see figure above).
The phenomenon was explained by Ludwig Prandtl in terms of his boundary layer theory. Reynolds had found that found that as the speed increases, the flow changes from laminar to turbulent. Prandtl argued that the turbulence mixes rapidly-moving external air into the boundary layer, increasing the range over which it adheres to the surface, making the trailing low pressure wake smaller and thereby reducing the drag force.
So, what's the deal?
Dimples! By roughening the surface of the golf ball, the critical Reynolds number is reduced to about 50,000, speeds that is achievable for a golfer. The dimples cause a transition to turbulence at a lower Reynolds number and result in reduced drag which can even double the flying distance compared to a smooth golf ball.

Scientists have used the Navier-Stokes equations to compute the flow around objects for a long time. In the case of a compressible Newtonian fluid, the Navier-Stokes equations look as follows:

A study by Asai & Seo investigated the critical Reynolds number of the Roteiro, Teamgeist II, Jabulani, and Tango 12.

The flight trajectory simulation suggests that the Tango 12, one of the newest soccer balls, has less air resistance in the medium-speed region than the Jabulani and can thus easily acquire large initial velocity in this region.
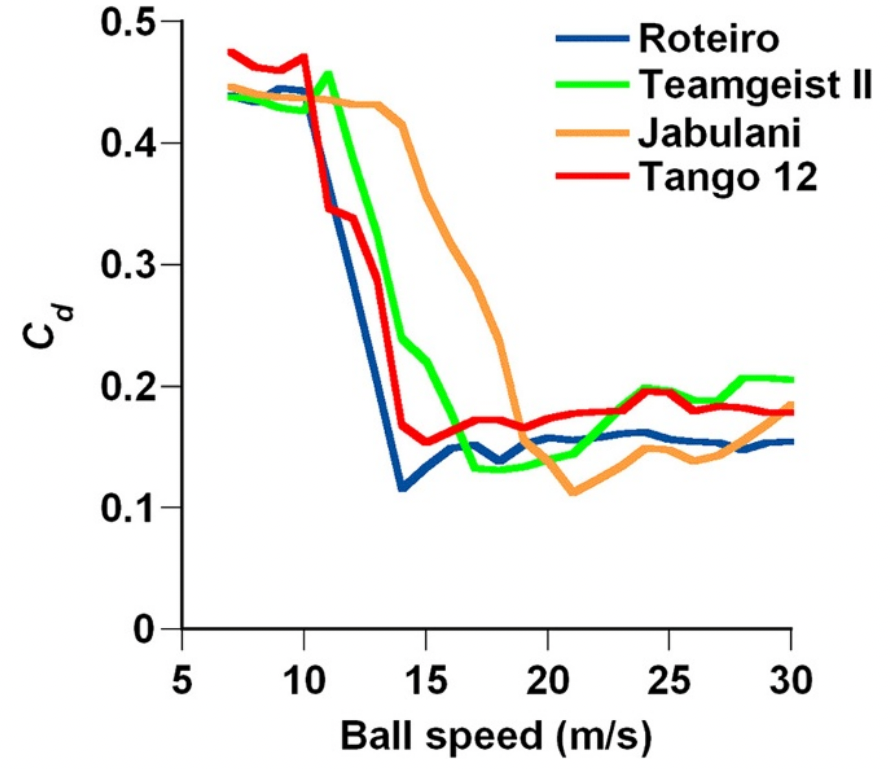
The critical Reynolds number of a soccer ball, as considered within the scope of this experiment, may depend on the extended total distance of the panel bonds rather than the small designs on the panel surfaces.
Let's compare the air flow over a football at two different speeds. When air flows over a ball, it behaves different than flowing over a smooth surface. The flow detaches from the surface of the football (flow separation), creating an area of low pressure behind (in the wake of) the ball.
The induced low pressure region creates a drag force that slows the ball. At low speeds, the air flow is laminar and separates early, creating a large wake and relatively high drag force. As speed increases the air becomes more turbulent (chaotic) which helps it stick to the ball for longer, reducing the size of the wake and lowering drag force.
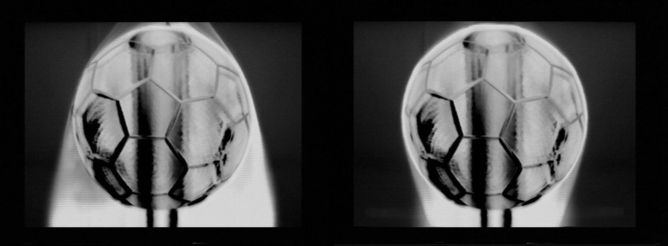
The seams "prevent" the air entering the “low drag” mode at low speeds. A perfectly smooth football would be unplayable (think about the predictability of a beach ball trajectory...horrible!) as the ball can experience different flow behaviours over different regions of its surface resulting in asymmetrical forces "shaking" the ball in different directions.
So what happened to the Jabulani? 🤔
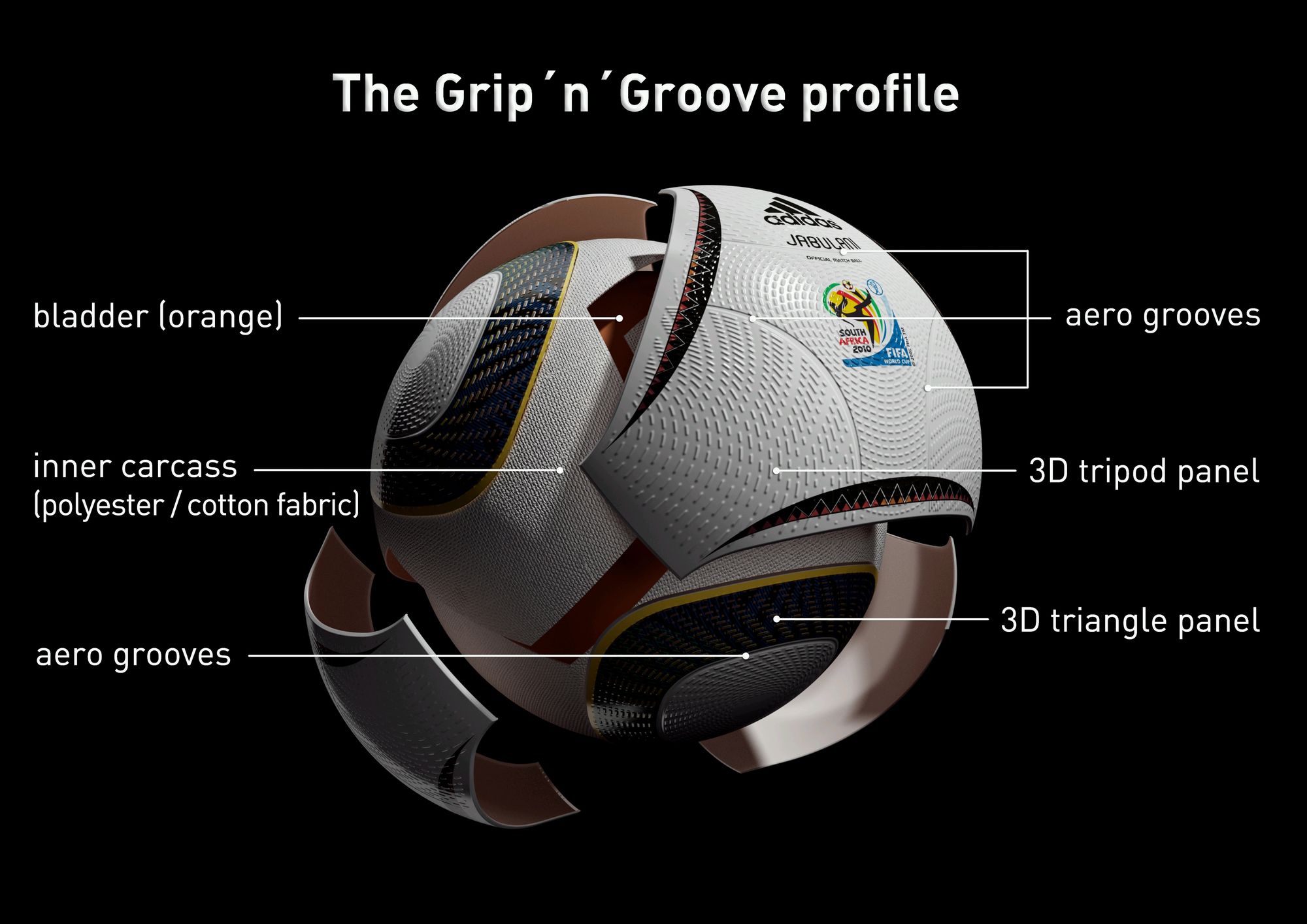
The aim of the designers at Adidas and scientists at Loughborough University was it to create a ball with favourable aerodynamic characteristics and perfect roundness at the same time – two opposing objectives as we now know. Adidas has reduced the number of panels to 8, each of which is thermally bonded and moulded in 3D before construction resulting in an incredibly round ball. To counteract the negative aerodynamic effects, a series of aero grooves have been added to each panel (see figure below). Their purpose is to stir the air flowing over the ball and try to ensure that flow is uniform. Did this help?
Caltech Scientists have also analysed the aerodynamic characteristics of the Jabulani. Although there is no data to compare, they do say:
Still, the Jabulani isn't so unpredictable that players can't learn to control it. "It seems like anytime the ball is changed, it takes a while for people to adapt," McKeon says. Source
This suggests that the Jabulani ball isn’t that unpredictable after all and it might just take time for players to adapt to its behaviour.
.... NASA has joined the chat!
On their web page, they describe strange aerodynamics of smooth balls but it is not clear whether they are referring to the Jabulani or Teamgeist. However, there's an interesting quote towards the end of the article:
From his research on tennis and cricket balls in wind tunnels, Mehta believes that the Jabulani ball will tend to knuckle at 45 to 50 mph, which coincides with the speed of the ball during free-kick around the goal area.
The Reverse Magnus Effect ⏪
In specific conditions, a flying spinning ball deflects in a direction opposite to that predicted by the Magnus Effect, which is known as the inverse or reverse Magnus effect. This (rather counterintuitive) phenomenon occurs because the boundary layer flow moving against the surface of a rotating sphere undergoes a transition to turbulence, whereas that moving with the rotating surface remains laminar.
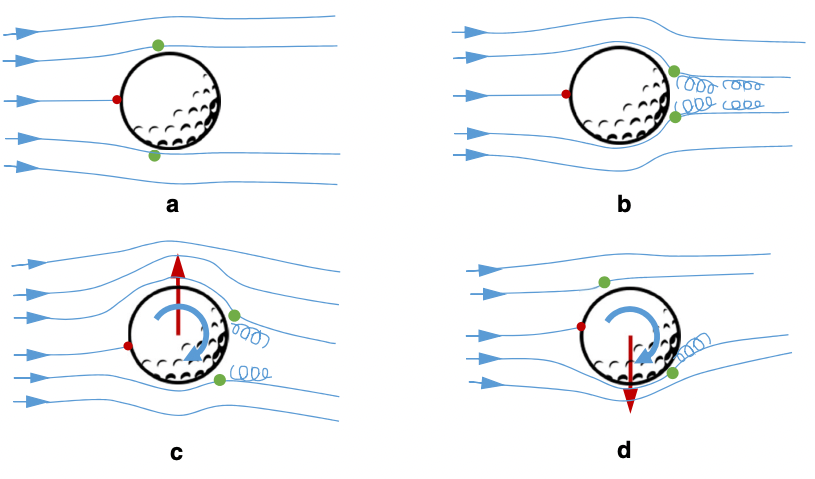
One study has shown a negative lift force on a sphere with backspin, the reverse Magnus effect. When the ball is traveling near the speed where the boundary layer becomes turbulent, backspin can cause the top side of the ball to have laminar flow, while the bottom boundary layer is turbulent, as shown in 1d in the figure above.
The laminar flow on the top surface moves the separation point forward, changing the direction of the Magnus effect downward, producing the reverse Magnus effect. Only a few studies have observed the reverse Magnus effect due to the small range of speed and spin rate where it occurs.
Using the wind tunnel, Bearman and Harvey found the reverse Magnus efect on scaled model golf balls at low speed (13.7 m/s) and low spin rate (<1500 rpm). The reverse Magnus effect was found numerically and experimentally on smooth balls & Bush found that the reverse Magnus effect on smooth spheres occurred in the drag crisis region. Source
The Flettner Rotor 🚢
The Magnus effect is not only used to calculate the trajectory of a football but can be used to change the direction of whole ships, also known as the Flettner Rotor.

These ships are equipped with one or more cylinders that can survive despite side winds. The interaction between the rotor surface and the wind flow creates a buoyancy force, giving a ship additional thrust. This not only saves fuel, but also reduces emissions. Rotors were developed as early as the 1920s, but did not catch on at the time due to the low price of oil. However, greater environmental awareness and rising fuel prices have made this type of propulsion interesting again in recent years.
Bonus: Newton's Laws of Motion in Football 📜
Assuming you have no idea about physics or forgot all laws, let's have a quick intro to Newton's three laws of motion.
Newton's First Law of Motion (Inertia)
According to Newton’s 1st law of motion, any object in motion, will stay in motion and any object at rest, will remain at rest unless acted on by an unbalanced force.
👉 In football, that unbalanced force is your foot, your head, gravity and the goal net that changes the balls motion. The ball is first at rest and has to be accelerated by muscle force.
Newton's Second Law of Motion (Force)
The change in velocity (acceleration) with which an object moves is directly proportional to the magnitude of the force applied to the object and inversely proportional to the mass of the object.
Mathematically, this is more commonly known as
\[ F = ma \]
👉 Applied to football, that simply means that we need more force to kick a ball faster.
Newton's Third Law of Motion (Action & Reaction)
Whenever one object exerts a force on another object, the second object exerts an equal and opposite on the first.
Or simple: "For every action, there is an equal and opposite reaction!"
If you're interested in aircrafts, you might appreciate this short movie featuring Orville and Wilbur Wright having a discussion about Newton’s Laws of Motion.
If you’d like to see more simulation or fluid dynamics related blogs like this one, consider subscribing to my latest blogs, tutorials and course updates - and please feel free to leave a comment down below! 🙂
Keep engineering your mind! ❤️
Jousef